Introduction
Yesterday night I was bored. I enjoy solving Sudokus by hand and wondered for quite some time how I could do it programmatically. Sure, a LLM could give me the answer in no time, but where would be the fun in that? Lets hop in.
What is Sudoku?
Sudoku is a logic-based number-placement puzzle. The objective of classic Sudoku is to fill a 9x9 grid with numbers in a way that all of those rules are true:
-
each row must contain exactly one of each digit (1-9)
-
each column must contain exactly one of each digit (1-9)
-
each subgrid must contain exactly one of each digit (1-9)
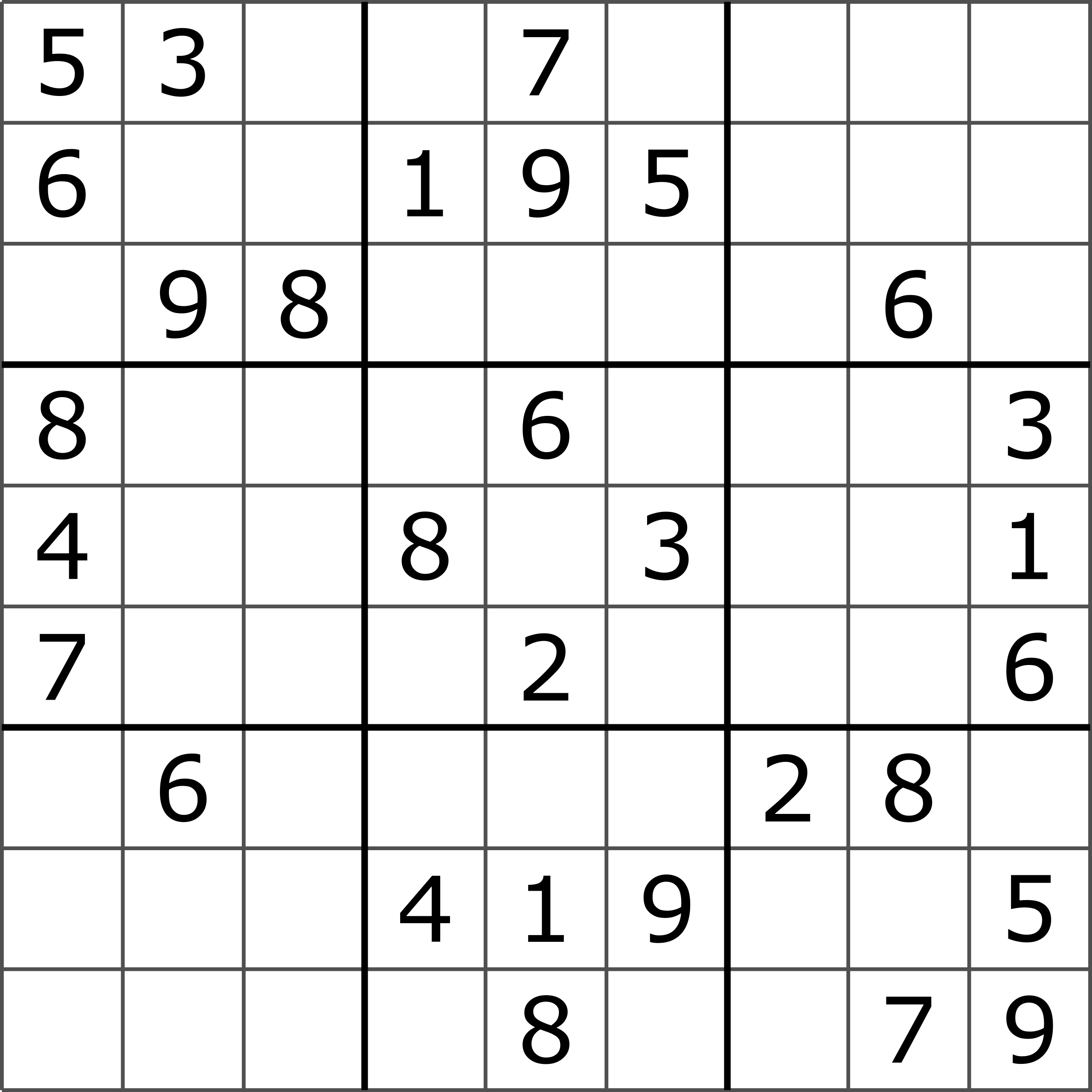
A start grid could look like this
How I usually solve Sudoku
I'd generally look for subgrids, rows or columns first that have the most prefilled digits. Then I'd look for a cell where only one digit can fit. If I can't find one like this, I go on, select a field, and just try inserting one of the possible digits and look wether it leads to something. That can get quite time consuming with the increasing complexity of a starting grid.
How we could let a computer do it
Now, always scanning for the cell with the least options could get very complex and might result in incredibly long backtracking chains, because the order of fields we try would probably often be completely random, such it might take a very long time to recognise we made an error.
I took the approach of scanning each row top to bottom for the first empty cell. While it doesn't eliminate the risk of long backtracking, I think it reduces it a bit, because its more likely to get multiple dependant cells in a row.
Where do I get the puzzles from?
While I could type out examples cell by cell, it would be a tideous process. So i looked for an API that provides sudoku puzzles. I ended up using the youdosudoku api.
SudokuField is a 2D array:
typealias SudokuField = [[Int]]Required Data Structures:
//I overdid error handling a bit for a script
enum FetchError: Error {
case urlCreation
case encoding(EncodingError)
case decoding(DecodingError)
case network(Error)
case api
case parse
}
//The api provides multiple difficulty levels
enum Difficulty: String {
case easy
case medium
case hard
}
//The parameters for the API Request
struct APIParams: Codable {
var difficulty: String
var solution: Bool = true
var array: Bool = false
}
//The structure of the API response
struct APIResponse: Codable {
var difficulty: String
var puzzle: String
var solution: String
}The fetching function:
//We can specify which difficulty we want the puzzle to be
func getSudokuField(difficulty: Difficulty) async -> Result<SudokuGame, FetchError> {
guard let url = URL(string: "https://youdosudoku.com/api/") else { return .failure(.urlCreation)}
var request = URLRequest(url: url)
do {
//encode the API Parameters
request.httpBody = try JSONEncoder().encode(
APIParams(difficulty: difficulty.rawValue)
)
request.httpMethod = "POST"
//fetch Data
let (data, response) = try await URLSession.shared.data(for: request)
//make sure the api responds with "OK"
guard let response = response as? HTTPURLResponse, response.statusCode == 200 else {
return .failure(.api)
}
//decode the response
let decoded = try JSONDecoder().decode(APIResponse.self, from: data)
//parse the field strings
//(e.g. "063010080010004000000020003200000008500692417000500900900703060100000000000050000")
//to a two dimensional Integer Array
guard let unsolved = parseField(decoded.puzzle),
let solved = parseField(decoded.solution) else { return .failure(.parse)}
//returning a game instance from the fetched data
let game = SudokuGame(
difficulty: Difficulty(rawValue: decoded.difficulty) ?? .medium,
puzzle: unsolved,
solution: solved
)
return .success(game)
//handling various errors
} catch let error as EncodingError {
return .failure(.encoding(error))
} catch let error as DecodingError {
return .failure(.decoding(error))
} catch {
return .failure(.network(error))
}
}
Parsing the string:
func parseField(_ field: String) -> SudokuField? {
var result = SudokuField()
var currentLine = [Int]()
var counter = 0
for char in field.map({ String($0) }) {
counter += 1
guard let number = Int(char) else { return nil }
currentLine.append(number)
//line is ended
if counter % 9 == 0 {
result.append(currentLine)
currentLine = [Int]()
}
}
return result
}Solving the Puzzle
Now that we got our inputs and don't have to do 'manual labor' anymore, we can start worrying about solving the Sudoku.
Typealiases:
typealias SudokuRow = [Int]
typealias Position = (SudokuField.Index, SudokuRow.Index) //coordinates of a cell
As I mentioned in How we let a computer do it we need to find the first empty cell:
func findFirstEmptyField(field: SudokuField) -> Position? {
//Find first row that contains an empty field
guard let rowIndex = field.firstIndex(where: {
$0.contains(0)
}) else { return nil }
//get the row
let row = field[rowIndex]
//find the first empty field in that row
guard let colIndex = row.firstIndex(of: 0) else { return nil }
return (rowIndex, colIndex)
}Great. Now we need to know which numbers we could put in:
func findPossibleValues(pos: Position, field: SudokuField) -> [Int] {
var possible = (1...9).map {$0}
//remove all values existing in the cells row
for num in field[pos.0] {
removeFromPossible(num: num)
}
//remove all values existing in the cells column
for row in field {
let num = row[pos.1]
removeFromPossible(num: num)
}
//get the coordinates where the subgrid – the cell is in – starts
let subgridStartPos = getSubgridStartIndex(pos: pos)
//iterate over the tree rows of the subgrid
for i in subgridStartPos.0 ..< subgridStartPos.0 + 3 {
//if the row is the same where the cell sits in, we don't need to check again
if i == pos.0 { continue }
let line = field[i] //get the row
//iterate over the 3 cells in the current row of the subgrid
for y in subgridStartPos.1 ..< subgridStartPos.1 + 3 {
//if the columns is the same where the cell sits in, we don't need to check again
if y == pos.1 { continue }
let num = line[y]
removeFromPossible(num: num)
}
}
//return all the numbers the cell could contain
return possible
//coordinate of the top left cell in a subgid
func getSubgridStartIndex(pos: Position) -> Position {
let row = startFor(value: pos.0)
let col = startFor(value: pos.1)
return (row, col)
//3 coordinates always have the same subgrid
func startFor(value: Int) -> Int {
switch value {
case 0, 1, 2: 0
case 3, 4, 5: 3
default: 6
}
}
}
//remove a given number from the possible values
func removeFromPossible(num: Int) {
guard num != 0 else { return }
possible.removeAll(where: {$0 == num})
}
}Of course you could do it by adding possible values instead of removing impossible, but since this aligns more of my personal thought process when solving by hand, I did it like this.
Alright, now we can finally solve the Sudoku!
We will use a recursive function that backtracks. That means we try a value in a cell and proceed with it as it was the right one. If later turns out we made a mistake, we got back to the mistake and try the next number. We will use inout as it lets all the function calls appearing work on the same grid.
//tell the function the current value is wrong
enum SolveError: Error {
case backtrack
}
func solve( field: inout SudokuField) -> Result<SudokuField, SolveError> {
guard let coords = findFirstEmptyField(field: field) else {
return .success(field)
}
let (row, col) = coords
let possibleValues = findPossibleValues(pos: coords, field: field)
//if there are no possible values, although the cell is empty, we made an error
guard !possibleValues.isEmpty else { return .failure(.backtrack) }
for value in possibleValues {
field[row][col] = value
switch solve(field: &field) {
case .success(let field):
return .success(field)
case .failure(let error):
continue
}
}
field[row][col] = 0
return .failure(.backtrack)
}
You can call it like that:
switch await getSudokuField(difficulty: .hard) {
case .success(let response):
var field = response.puzzle
let solution = solve(field: &field)
switch solution {
case .success(let success):
print(format(field: success))
print(format(field: response.puzzle))
default:
break
}
case .failure(let error):
print(error)
}To look better when printed in console, I added a formatting function:
func format(field: SudokuField) -> String {
var output = "┏---┳---┳---┳---┳---┳---┳---┳---┳---┓"
for x in 0..<9 {
output.append("\n|")
for y in 0..<9 {
output.append(" \(field[x][y] != 0 ? "\(field[x][y])": " ") ")
output.append("|")
}
if x < 8 {
output.append("\n┣---╋---╋---╋---╋---╋---╋---╋---╋---┫")
}
}
output.append("\n┗---┻---┻---┻---┻---┻---┻---┻---┻---┛")
return output
}Result:

How does this algorithm look when executed?
I know it might be quite hard to understand how recursion with backtracking actually looks, so I made a quick app, that visualizes the solving:

In the gif you see how it goes deeper until it encounters that an error was made. Then it tracks back as far as needed and tries again.
Benchmarks
Because I was still a little bored and curious how fast this actually was, I proceeded to write a small benchmark. (sorry to youdosudoku for spaming your api, a batch endpoint would be great).
//specifiy how many sudokus we want to solve
func benchmark(amount: Int) async {
var challenges = [SudokuGame]()
guard amount > 0 else { return }
//prefetch all puzzles to only test how long it actually takes to solve a puzzle, not including a fetch
for _ in 1...amount {
switch await getSudokuField(difficulty: .hard) {
case .success(let game):
challenges.append(game)
default: continue
}
}
var accumulatedTimes = [UInt64]()
for game in challenges {
let startTime = DispatchTime.now() //take time when it starts
var field = game.puzzle
_ = solve(field: &field)
let endTime = DispatchTime.now() //take time once its solved
//calculate how long it took
accumulatedTimes.append((endTime.uptimeNanoseconds - startTime.uptimeNanoseconds))
}
//sort to easily get slowest, fastest and median
accumulatedTimes.sort()
var total: UInt64 = accumulatedTimes.reduce(0, {$0 + $1})
print("solved \(accumulatedTimes.count) sudokus in an average time of \(Double(total / UInt64(challenges.count)) / 1000000.0)ms, \(Double(total) / 1000_000.0)ms total")
print("slowest: \(Double((accumulatedTimes.last ?? 0)) / 1000000.0)ms")
print("fastest: \(Double((accumulatedTimes.first ?? 0)) / 1000000.0)ms")
print("median: \(Double((accumulatedTimes[accumulatedTimes.count / 2] ?? 0)) / 1000000.0)ms")
}I called it with 1000 sudokus to solve, that should be reasonably representative without spaming the api too much. (PLEASE be responsible and don't do this yourself. I don't want them to get crushed by thousands of requests of readers)
To be honest, I expected it to be faster than me (obviously) but not by that much. Remember: they're all of the difficulty "hard".
solved 1000 sudokus in an average time of 2.926511ms, 2926.511704ms total
slowest: 34.77025ms
fastest: 0.554625ms
median: 1.7765msOne Million per hour
I now was interested how many I could do in an hour. The result suggests about 333 per second:
(~ 3000ms for 1000 sudokus -> 1000 / 3 = 333.33)
333 * 3600 = 1.198.800
So there you go, over a million solves per hour :)
Conclusion
Writing a recursive, backtracking algorithm to solve Sudoku was easier than I thought. I'm pretty sure there are faster ways to solve them, but I don't really see a reason to optimize further. Or when did you last need to solve a million in less than an hour?
It also was a fun excursion, because I rarely do such theoretical stuff.
Props to Swift as well for being that fast.
If you enjoyed the read I would appreciate you sharing it.
Until next time, Mia