I'm a very curious person. This weekend I wondered how compression actually works. Whats the best way to understand something in the programming-world? Exactly, to code it. So I did.
Research
To decide which compression algorithm I want to look into I had to do some research of what exists and is commonly used. To give you an overview and better explain why I chose Huffman, here are some common compression algorithms
- Lempel-Ziv-Welch (LZW)
- replaces repeating sequences of bytes with codes of fixed length, mapped in a dynamic dictionary
- known for application in GIF and early Version of TIFF
- LZ77 & LZ78 (Basis of LZW)
- LZ77: Searches for repeating sequences in a sliding window on the already processed text and replaces them through a reference to their earlier occurence (distance and length)
- LZ78: Builds an explicit dictionary of found phrases
- Basis of many modern compression methods (e.g. ZIP)
- Deflate
- Combination of LZ77 and Huffman-Coding
- LZ77 identifies and replaces seqences
- Huffman-Coding gets applied to the result of LZ77
- most known for usage in ZIP
- Run Length Encoding (RLE)
- replaces sequences of identical Bytes through a single byte instance + amount of repetitions
- most effective on Data with long sequences of identical bytes e.g. bitmap
- Huffman-Coding:
- the algorithm I decided to use
Why Huffman
You may wonder why I chose Huffman to implement. To get into compression, I expected 2 things:
- applicable to files I most often use: Code (Plaintext)
- relatively simple to understand and implement
Huffman vs RLE
While also being relatively easy to implement, RLE didn't meet my requirement of being applicable to plaintext. RLE is not a good fit, because in Code, JSON, XML,... you rarely have chains of a repeating character like:
AAABBBBBBBCCCDDDDDDDD -> RLE Result: A3B7C3D8Terminology
- Tree
- hierarchical datastructure
- consisting of nodes, connected by edge
- single root node, no cycles
- Complete Binary Tree
- each layer is completely filled, except the last one
- last level nodes are as far left as possible
- Huffman Tree
- full binary tree
- Heap
- complete binary tree
- often implemented with use of arrays
- O(1) for top lookup
- O(log n) for insertion and deletion
- Learn more
- min-heap
- heap where each parent node is smaller or equal than its child nodes
Node types in Kontext of a Huffman Tree (Full Binary Tree)
Let me explain what I mean by "node", keep in mind that this definition is only applicable to a Huffman-Tree (full binary tree).
(R)
/ \
(L) (I)
/ \
(L) (L)
Root Node (R)
Leaf Node (L)
Internal Node (I)All nodes being at the bottom of a branch with no lower "connections" (children) to other nodes are called Leaf Nodes (L). Each Leaf Node has either an internal or the root node above it (parent).
There is only one Root Node (R), its the one at the top, from where the tree spreads. Its the origin and starting point, so it never has a parent node.
Every Node between a Leaf Node and the Root Node is an internal Node. An internal Node has either the Root Node or an internal Node as parent.
Both Root and internal Nodes must have exactly two children, each either Leaf Node or internal Node.
How does Compression work
Huffman Coding works through a tree. We count how often each character existing in the file appears. From the character to frequency map we create a Leaf-Node each.
Now we initialize a min-heap with all leaf nodes, using the frequency as priority indicator. If two leaf nodes got the same frequency, we prioritize the node with the "smaller" character (character mapping to the lower binary representation, usually handled automatically through the < > comparison).
This tie-breaking rule is essential depending on how you store your tree in the header. It ensures that the compression and decompression processes build the exact same Huffman tree, guaranteeing that the file can be correctly restored. Without a deterministic rule, different implementations might create different trees for the same input, making decompression impossible.
Now we pop the top two nodes from the heap and create an internal node, having the smaller node (automatically the first node we pop, because its a min-heap) on the left and the bigger on the right. The new nodes frequency is the sum of the two child nodes frequencies. Now we store the new node in the heap. This gets repeated until there is only one left. The last remaining node is the root of our Huffman-Tree.
Now we have to create a map. To do that, we iterate recursively over the tree while keeping track of our path. if we encounter a leaf node, we store the path in the dictionary for the character of the leaf node. Then we go back to the last Node where we got a path left we didn't go down yet.
Once we have our completed map, we just iterate over the whole file. We retrieve the path for the given character from our newly created dictionary and write a 0 bit for each left turn and a 1 for each right turn. In the end we add we add padding to the next full Byte.
Next we write a header to the output file, containing the Huffman tree and padding. Then we add the encoded bytes to the file and save it.
Congrats, your file is now compressed and depending on the size and contents of the file, you get about 50% compression.
How does Decompression work?
First we reconstruct the Tree. Then we iterate over body data bit by bit. We start at the root node and keep track of the node we're at.
Again, each 0 means we go to the left node and for a 1 we proceed to the right. Eventually we will always land on a leaf node. Once we're there, we append our decompress string by the character at the leaf node. Then we just reset our current node variable to the root node. Repeat until the amount of bits left equals the padding.
Write the result to a file, and your original contents should be exactly restored without any loss.
Compression Example
By now you're maybe wondering how a compressed string actually looks in binary. Lets say we take "Mississippi" as input. Mississippi contains:
- 1 M
- 2 p
- 4 i
- 4 s
I already ordered it in the overview above, so that would be the arrangement in the heap as well.
M & P are the least frequent characters. That leaves us with 3 as their parent node.
(Mp 3)
/ \
(M 1) (p 2)we insert Mp 3 into the Heap (in the real world you wouldn't name the node anything, thats just to make it easier to track for you):
- 3 Mp
- 4 i
- 4 s
now Mp and i are the least frequent 3 from Mp + 4 from i leaves us with seven:
(Mpi 7)
/ \
(Mp 3) (i 4)
/ \
(M 1) (p 2)we again insert the result node into heap:
- 4 s
- 7 Mpi
we only have two nodes left, so lets combine them into our root node
(sMpi 11)
/ \
(s 4) (Mpi 7)
/ \
(Mp 3) (i 4)
/ \
(M 1) (p 2)For s we go left(0) from the source node:
- s: 0 For i we have to go right(1) right(1):
- s: 0
- i 11 For M we go right(1) left(0) left(0):
- s: 0
- i 11
- M 100 And last but not least, for p we go right(1) left(0) right(1)
- s: 0
- i 11
- M 100
- p 101
now we replace each character with its corresponding bits
Before:
M i s s i s s i p p i
01001101 01101001 01110011 01110011 01101001 01110011 01110011 01101001 01110000 01110000 011010011 Byte (8 Bits) for each character. leaves us with 11 Bytes (88 Bits)
After:
M i ssi ssi p p i
10011001 10011101 10111000Compressed Mississippi is only 3 Byte big (21 Bits + 3 padding)
Compression (with code)
Lets look at how we would compress a string (for example read from a plaintext file).
First we need to count how often each character appears in our input String.
private func count(_ input: String) -> [Character: Int] {
// store all amounts with character as key
var counts = [Character: Int]()
// iterate over the string, counting each character
input.forEach { char in
// treat non-existing keys as having value 0
counts[char, default: 0] += 1
}
return counts
}Next, we create our Huffman-Tree.
func buildTree(
_ counts: [Character: Int]
) throws -> HuffmanNode {
// Convert KV pairs to leaf nodes
let leafNodes = counts.map { key, value in
HuffmanNode(character: key, frequency: value)
}
// initialize the Heap
let heap = Heap<HuffmanNode>{ lhs, rhs in
lhs.frequency < rhs.frequency
}
heap.add(leafNodes)
// repeat while more than the root node is left in heap
while heap.count > 1 {
// get and remove two smallest nodes
// smaller one is always left child
guard let leftNode = heap.popTop(),
let rightNode = heap.popTop() else {
break
}
// create new Huffman Node
// frequency gets calculated inside initializer
let node = HuffmanNode(
left: leftNode,
right: rightNode
)
// add new node into heap
heap.insert(item: node)
}
// get top returns nil if heap is empty
// we safely unwrap it
guard let top = heap.getTop() else {
//throw Error
}
return top
}
We need to map characters to a binary sequence:
// pass root node of Huffman Tree
func buildMap(root: HuffmanNode) -> [String: [Bool]] {
// Bool to represent 0 / 1
var map = [String: [Bool]]()
traverse(node: root, map: &map, currentPath: [])
return map
// recursively iterate over the tree
func traverse(
// next node
node: HuffmanNode,
// map variable to mutate
map: inout [String: [Bool]],
// the path we went to get to the node
currentPath: [Bool]
) {
// if we're at a leaf node, save path for character
if let char = node.character {
map["\(char)"] = currentPath
return
}
// If it's an internal node, continue traversal
// Go left: append 'false' (0) to the path
if let left = node.left {
// Create a copy of the path for this branch
var newPathForLeft = currentPath
newPathForLeft.append(false) // 0 for left
traverse(
node: left,
map: &map,
currentPath: newPathForLeft
)
}
// Go right: append 'true' (1) to the path
if let right = node.right {
// Create a copy of the path for this branch
var newPathForRight = currentPath
newPathForRight.append(true) // 1 for right
traverse(
node: right,
map: &map,
currentPath: newPathForRight
)
}
}
}Recursion is often a bit hard to understand. Let me break down how this works:
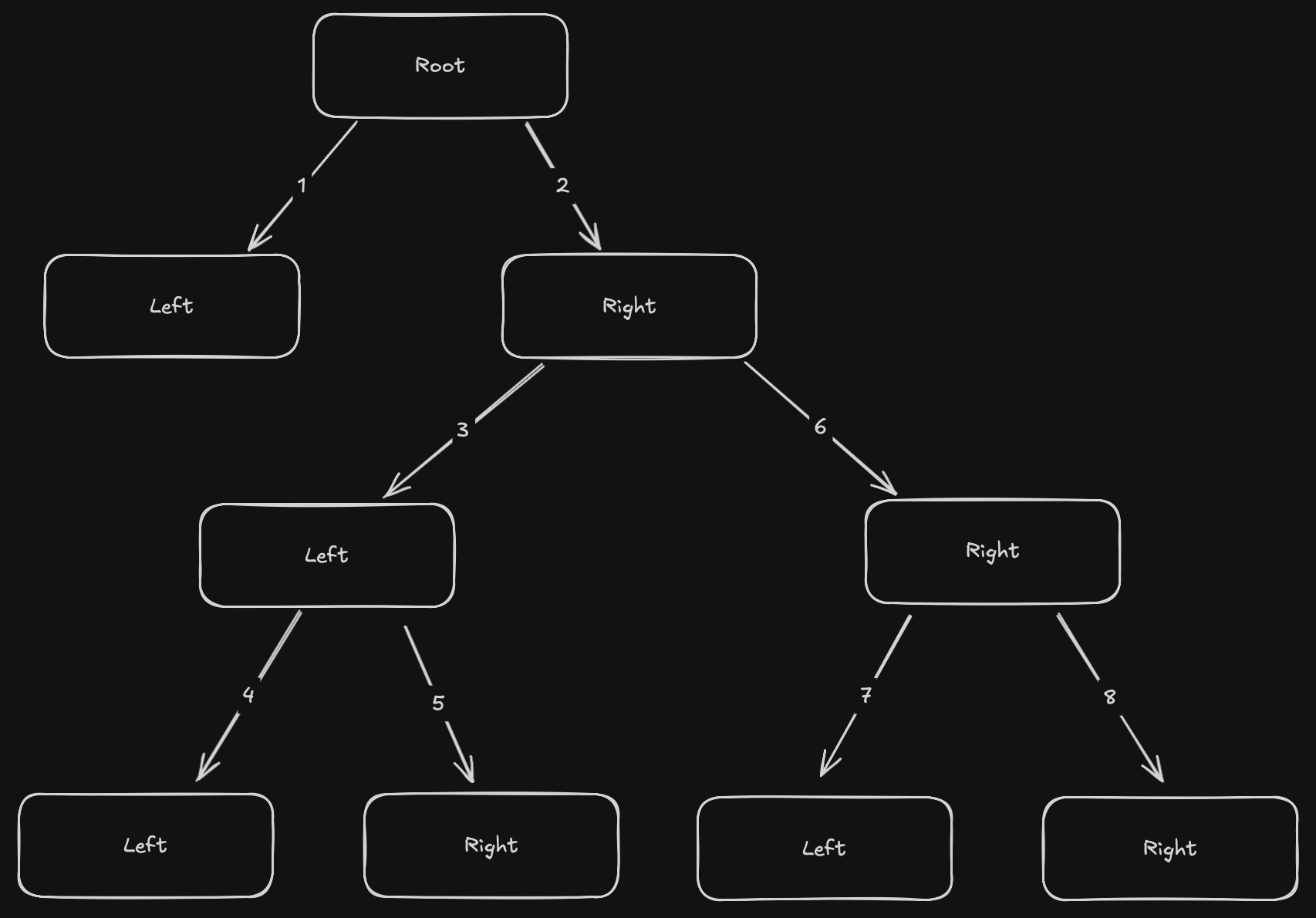
We go always as far left as possible.
Ok, great, we got our map, so its finally time to compress!
func compress(_ data: String) throws -> Data {
// how often does each character occur
let counts = count(data)
// build Huffman-Tree and store root
let treeRoot = try buildTree(counts)
// map each character to a bitsequence
let map = buildMap(root: treeRoot)
// swift doesn't have included bitwise writing
// so we're gonna use our own
var bitOperator = BitWriter()
// iterate over the whole to encode string
for char in data {
guard let sequence = map["\(char)"] else {
// character doesn't exist in map
// only typesafety artifact, should never happen
return
}
// write sequence bit by bit
for bit in sequence {
bitOperator.write(bit: bit)
}
}
// get compressed data + padding
let (data, padding) = bitOperator.getData()
// encode data including padding, tree and compressed data
// PropertyListEncoder has smaller output than JSON
return try PropertyListEncoder().encode(
KompressorFile (
h: .init(
p: padding,
t: treeRoot.serializeToCompactData()
),
b: data
)
)
}
struct KompressorFile: Codable {
///header
let h: Header
///body
let b: Data
struct Header: Codable {
///padding
let p: Int
///huffman root node (tree)
let t: Data
}
}A very important part: the Huffman-Node Datastructure. If you're not interested in those details [Jump to Decompression]
/// Represents a node in the Huffman tree. It can be either a leaf node
/// (containing a character and its frequency) or an internal node
/// (containing only a frequency and references to its children).
class HuffmanNode: Comparable {
let character: String? // Only set for leaf nodes
let frequency: Int
var left: HuffmanNode?
var right: HuffmanNode?
/// Initializes a leaf node.
init(character: Character, frequency: Int) {
self.character = "\(character)"
self.frequency = frequency
self.left = nil
self.right = nil
}
/// Initializes an internal node.
init(left: HuffmanNode, right: HuffmanNode) {
self.character = nil // Internal nodes don't represent a single character
self.frequency = left.frequency + right.frequency
self.left = left
self.right = right
}
/// Compares two HuffmanNodes based on their frequency, then by character for tie-breaking.
static func < (lhs: HuffmanNode, rhs: HuffmanNode) -> Bool {
if lhs.frequency != rhs.frequency {
return lhs.frequency < rhs.frequency
}
// Tie-breaking: If frequencies are equal, prioritize leaf nodes, then by character value.
// This ensures a deterministic tree.
if lhs.character != nil && rhs.character == nil {
return true // Leaf node (lhs) is "smaller" than internal node (rhs) for tie-breaking
} else if lhs.character == nil && rhs.character != nil {
return false // Internal node (lhs) is "larger" than leaf node (rhs) for tie-breaking
} else if let lhsChar = lhs.character, let rhsChar = rhs.character {
return lhsChar < rhsChar // Compare characters for leaf nodes
}
return false
}
static func == (lhs: HuffmanNode, rhs: HuffmanNode) -> Bool {
return lhs.frequency == rhs.frequency && lhs.character == rhs.character
}
}If you're interested in the Heap implementation, read the article (thanks, Tom) or have a look at the file
We need some additional helpers to keep the size of the tree small when saved in the compressed File. If you're not interested in those details [Jump to Decompression]
extension HuffmanNode {
/// Serializes the tree into a compact binary Data object using BitWriter.
func serializeToCompactData() -> Data {
var writer = BitWriter()
self.serialize(into: &writer)
// Use your getData() method to finalize the data buffer
return writer.getData().data
}
/// helper for recursive serialization.
private func serialize(into writer: inout BitWriter) {
if character != nil {
// 1. This is a leaf node. Write a '1' bit.
writer.write(bit: true)
// 2. Then, write the character's byte value.
guard let char = self.character?.first, let byte = char.utf8.first else {
// Fallback for an invalid leaf node.
writer.write(bits: 0, count: 8)
return
}
// Use the multi-bit write method for efficiency and clarity.
writer.write(bits: UInt(byte), count: 8)
} else {
// 1. This is an internal node. Write a '0' bit.
writer.write(bit: false)
// 2. Recursively serialize the left and right children.
left?.serialize(into: &writer)
right?.serialize(into: &writer)
}
}
}To write bitwise, we need our own implementation in swift. If you're not interested in those details [Jump to Decompression]
struct BitWriter {
/// The underlying buffer where bits are being accumulated.
private var data: Data
/// The current byte being filled with bits.
private var currentByte: UInt8
/// The number of bits already written into `currentByte`.
/// Ranges from 0 to 7.
private var bitsInCurrentByte: Int
/// Initializes a new `BitWriter`.
init() {
self.data = Data()
self.currentByte = 0
self.bitsInCurrentByte = 0
}
/**
Appends a single bit to the buffer.
- Parameter bit: The bit to append (true for 1, false for 0).
*/
mutating func write(bit: Bool) {
// Shift the current byte to the left to make space for the new bit
currentByte <<= 1
// If the bit is true (1), set the least significant bit
if bit {
currentByte |= 1
}
bitsInCurrentByte += 1
// If the current byte is full (8 bits), append it to the data buffer
// and reset for the next byte.
if bitsInCurrentByte == 8 {
data.append(currentByte)
currentByte = 0
bitsInCurrentByte = 0
}
}
/**
Appends a sequence of bits from a given `UInt` value.
The bits are taken from the least significant side of the value.
- Parameters:
- value: The `UInt` value containing the bits.
- count: The number of bits to take from the `value` (starting from LSB).
Must be between 0 and `UInt.bitWidth`.
*/
mutating func write(bits value: UInt, count: Int) {
// Input validation
precondition(
count >= 0 && count <= UInt.bitWidth,
"Count must be between 0 and \(UInt.bitWidth)."
)
// Iterate from the most significant bit of the 'count' bits down to the least significant.
// This ensures bits are written in the correct order (MSB first).
for i in (0 ..< count).reversed() {
// Check if the i-th bit (from right) is set in the value.
let bit = (value >> i) & 1 == 1
write(bit: bit)
}
}
/**
Returns the accumulated `Data` buffer.
- Returns: The `Data` object containing the packed bits.
This method also handles any remaining bits in `currentByte`
by padding with zeros.
*/
mutating func getData() -> (data: Data, padding: Int) {
// If there are any remaining bits in currentByte,
// we need to pad it with zeros to fill the byte
// and append it to the data buffer.
if bitsInCurrentByte > 0 {
// Shift remaining bits to the left to align them to MSB of the byte
// and effectively pad with zeros from the right.
currentByte <<= (8 - bitsInCurrentByte)
data.append(currentByte)
currentByte = 0
bitsInCurrentByte = 0
}
return (data: data, padding: bitsInCurrentByte == 0 ? 0: (8 - bitsInCurrentByte))
}
}Decompression (with code)
Decompressing is a lot simpler, as we only have to rebuild the tree and run over it.
func decompress(_ file: KompressorFile) throws -> Data {
let tree = HuffmanNode(fromCompactData: file.h.t)
var reader = BitReader(data: file.b)
var reconstructed = ""
var currentNode = tree
while reader.remainingBits > file.h.p {
if let char = currentNode?.character {
reconstructed.append(char)
currentNode = tree
}
guard let bit = reader.readBit() else {
break
}
guard let nextNode = bit ? currentNode?.right: currentNode?.left else {
throw E.internalError(description: "Unexpectedly encountered leaf node")
}
currentNode = nextNode
}
guard let reconstructedData = reconstructed.data(using: .utf8) else {
//error Decoded string isn't convertible to utf8
return
}
return reconstructedData
}We also need a new initializer to create our tree from compacted data. Jump to Conclusion
extension HuffmanNode {
/// Deserializes a HuffmanNode from a compact binary Data object.
convenience init?(fromCompactData data: Data) {
guard !data.isEmpty else { return nil }
var reader = BitReader(data: data)
// The recursive helper will build the entire tree.
guard let reconstructedNode = HuffmanNode.build(from: &reader) else {
return nil
}
// Use the reconstructed node's properties to initialize self.
self.init(
character: reconstructedNode.character?.first,
frequency: reconstructedNode.frequency,
left: reconstructedNode.left,
right: reconstructedNode.right
)
}
/// Private helper for recursive deserialization.
private static func build(from reader: inout BitReader) -> HuffmanNode? {
guard let bit = reader.readBit() else { return nil }
if bit == true { // Leaf node
guard let byte = reader.readByte() else { return nil }
let char = Character(UnicodeScalar(byte))
// Frequency is not stored and not relevant anymore
// so we use a placeholder
return HuffmanNode(character: char, frequency: 0)
} else { // Internal node
guard let leftChild = build(from: &reader),
let rightChild = build(from: &reader)
else {
return nil
}
return HuffmanNode(left: leftChild, right: rightChild)
}
}
// Helper initializer to construct a node from its components.
private convenience init?(character: Character?, frequency: Int, left: HuffmanNode?, right: HuffmanNode?) {
if let char = character {
self.init(character: char, frequency: frequency)
} else if let l = left, let r = right {
self.init(left: l, right: r)
} else {
return nil
}
}
}And of course we need a possibility to read bit by bit too. Jump to Conclusion
struct BitReader {
private let data: Data
private var byteIndex: Int
private var bitPosition: Int// 0-7, from MSB to LSB
var remainingBits: Int
init(data: Data) {
self.data = data
self.byteIndex = 0
self.bitPosition = 0
self.remainingBits = data.count * 8
}
/// Reads a single bit from the buffer.
/// Returns nil if no more bits are available.
mutating func readBit() -> Bool? {
guard byteIndex < data.count else { return nil }
let currentByte = data[byteIndex]
// Read bit from left (MSB) to right (LSB)
let bit = (currentByte >> (7 - bitPosition)) & 1 == 1
bitPosition += 1
remainingBits -= 1
if bitPosition == 8 {
bitPosition = 0
byteIndex += 1
}
return bit
}
/// Reads a full 8-bit byte from the buffer.
/// inverse of `BitWriter.write(bits:count:8)`.
mutating func readByte() -> UInt8? {
var byte: UInt8 = 0
// We need to read 8 bits to form a byte.
// The first bit read corresponds to the MSB of the original byte.
for i in (0..<8).reversed() {
guard let bit = readBit() else {
// Not enough bits left to form a full byte
return nil
}
if bit {
byte |= (1 << i)
}
}
return byte
}
}Conclusion
Thank you so much for sticking through. It was a lot of fun to learn how this works. I hope you learnt something too.
Now I'm very curious how LZ77 works, maybe I'll write about it too.
If you're interested to see how all this looks as a cli-tool, hop over to my github.
If you enjoyed the read I would appreciate you sharing it.
Until next time, Mia
Sidenote
The repo and cli are called "kompressor" because I once got a plushie cat. It arrived vacuum packaged and never completely "uncompressed" so it got called Kompressor.